Self-Similar Fractals: Quilts and the Sierpinski Triangle

This is the first in what I hope will be a sporadic series explaining some of the math behind certain kinds of fractals.  (Well, I hope it will be a series; I don't hope specifically that it will be sporadic, but I'm sure that if it is a series it will be sporadic.)

Self-Similarity
One of the non-technical definitions of "fractal" is "self-similar, and infinitely detailed".  Self-similar means that the parts are similar to the whole; as you zoom in on one part of the fractal, you keep finding properties similar to the properties of the entire fractal.  This can be exhibited in a lot of different ways (there are a lot of different properties with respect to which an object coul be self-similar), and not all fractals have the exact kind of self-similarity I'm writing about in this post.  In this post, I'm writing about fractals that are made up of scaled down, but otherwise exact, copies of the whole thing.

Sierpinski Triangle
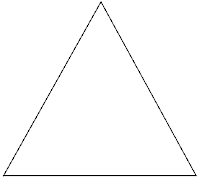
Start with a triangle.

In order to be self-similar, it has to be made up of smaller copies of itself.  So turn it into a trangle made out of triangles.

But now those smaller triangles aren't really copies of the whole thing, because the whole thing is made up of smaller triangles, whereas the smaller triangles are just plain triangles!  So, make them into triangles made up of even smaller triangles.

But now the even smaller triangles aren't really copies of the whole thing, because the whole thing is made up of smaller and even smaller triangles, whereas the even smaller triangles are just plain triangles!  So, make them into triangles made up of yet smaller triangles.   But...  won't we end up with the same problem?  Yup.  So what do we do?  Keep going till infinity.

And now in the pursuit of perfect self-similarity, we've also got infinite detail.  And that is the Sierpinski Triangle, a fractal named after Wacław Sierpiński.

Quilts
We can do the same kind of process with other shapes to make more cool fractals.  One pattern that I've been playing with recently looks like it would make a neat quilt pattern:

It's made by starting with a square and turning it into smaller squares, and then doing that to each smaller square, like so:

 If I mix things up a bit, and at some steps turn squares into hexagons or circles that have new rules for turning into more circles, hexagons, or squares, I can get things like this:

Some Math
I said before that "self-similar and infinitley detailed" was a non-technical definition of fractal.  There are several technical definitions, and they aren't entirely consistent (a topic for another post?), but the one I'm going to go with is "a set whose Hausdorff dimension is strictly greater than its topological dimension".  (This is the definition Benoit Mandelbrot used (see The Fractal Geometry of Nature).)  If you know about sets and dimensions already, then you have an idea what that means; if you don't, I'll try to explain.

Topological dimension is a usually intuitive notion of dimension that we usually mean when we say "dimension". Look at your hand.  Think about all the points in space that your hand occupies.  That set of points is three-dimensional.  The image represented by the lights of your computer screen, on the other hand, is two-dimensional.  A squiggly (or non-squiggly) line is one-dimensional.  These are topological dimensions.  But, what is the dimension of the Sierpinski Triangle?  Well, it's made up of a bunch of line segments, so its topological dimension is 1.  But we add infinitely many line segments, and it keeps getting denser and denser - might this make the dimension get bigger?  But then, it's never as dense as a filled-in plane... what if we decided to try something wacky and allow dimensions between 1 and 2?  Just to see what would happen?  Hausdorff dimension does just that.  Your hand's Hausdorff dimension is still 2, unless you're an awesome mutant with a fractal hand, in which case I'd love your autograph but I'm not sure you'd be able to write it.  My point is, Hausdorff dimension usually is the same as topological dimension, except in pathological cases (fractals).  The actual definition of Hausdorff dimension is a topic for another time, but I'll write now about how to find the Hausdorff dimension of exactly self-similar fractals (which is a lot easier than in general).

The Hausdorff dimension of an exactly self-similar fractal is found by solving the following equation (called a Moran equation) for $s$:

\[  \sum c_i^s = 1 \]

The $c_i$ terms are the scaling ratios for the self-similarity.  For example, in the Sierpinski Triangle, the whole set of points is made up of three copies of itself, each of which is scaled down to 1/2 the size of the whole, so $c_1 = c_2 = c_3 = $ 1/2.

The Moran equation for the Sierpinski Triangle, then, is
\[ 3\left(\frac{1}{2}\right)^s = 1 \text{, or } \left(\frac{1}{2}\right)^s = \frac{1}{3} \]
We can take the logarithm of both sides and get $ \log(\frac{1}{2})^s = \log\frac{1}{3}$, and then use properties of logs to get $ s = \log\frac{1}{2}/\log\frac{1}{3}$ which is the same as $\frac{\log{3}}{\log{2}}$.  Plug that into wolframalpha, and we find that $ s = $ 1.584962..., and that is the Hausdorff dimension.  Since this is definitely greater than 1, the topological dimension of the Sierpinski Triangle, it is a fractal.

We can do the same thing with my quilt fractal.  It's made up of five copies itself, four of which are scaled down to 1/4 the size, and one (the middle, tilted one) scaled to $(1/\sqrt{2})$ the size.  So the Moran equation is
\[ 4\left(\frac{1}{4}\right)^s + \left(\frac{1}{\sqrt{2}}\right)^s = 1. \]
This is a lot harder to simplify by hand but fortunately wolframalpha can take it from here and give us $s =$ 1.6121...  So that's the Hausdorff dimension of the quilt fractal.  I haven't figured out yet how to apply this to the mixed up hexagon/circle/square fractals.