More Quilts & Sierpinskis!

Thinking about fractals and quilt patterns led me on a google search, which resulted in finding this page - Quilts and Famous Curves - about some real quilts made with fractal patterns.

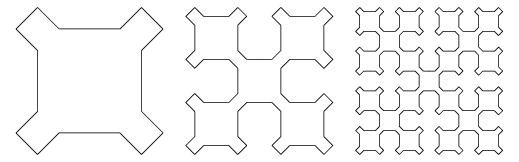
As far as I can tell, the Sierpinski curve featured doesn't have anything to do with the Sierpinski triangle except that they were both described by the same guy.  Here's a diagram of an alternative method of construction (basically just skipping every other step in the construction given on the quilt page):

Weisstein, Eric W. "Sierpiński Curve." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/SierpinskiCurve.html

You can't directly apply the Moran equation method to find its dimension, because the scaled-down copies that compose the whole overlap with each other a little, and the Moran equation only necessarily holds when they are non-intersecting

According to wikipedia, the curve is space-filling, which means that in the limit as n (the number of iterations of fractalization) goes to infinity, the curve fills up the unit square completely.  This means its Hausdorff dimension is 2, while its topological dimension is 1.  One definition of fractal requires that a fractal have non-integral Hausdorff dimension, so under that definition, the curve isn't really a fractal.  Personally I think Mandelbrot's definition (mentioned in my last post), where a fractal merely has greater Hausdorff than topological dimension, is a lot more useful, because of shapes like this; this shape is certainly not normal, so I think we might as well throw it in with the fractals.  But that's just semantics.

That wikipedia page also says that this curve has been used to make an approximation algorithm for the Travelling Salesman Problem (pretty cool!); it also has some java and logo code for drawing the curve if you're interested.

If you're interested in seeing more mathematical quilts, here is the homepage for one of the authors of the book featured in the first link.  There are lots of neat pictures.

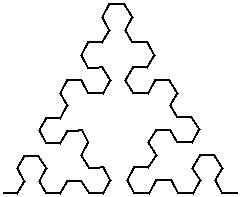
P.S. There is a another fractal curve similar to this one that is directly related to the Sierpinski triangle.  It starts out like this:

 Turn it into a bump made out of bumps:

 And turn each of those bumps into smaller bumps:

Do you see where this is going?

It's the Sierpinski triangle!

(9 iterations)

It's a little bit intuitive, since you are turning the shape into 3 half-size copies of itself at each step, just like in the other construction.  But the shape and placement of the copies does matter; for example, the following fractal is also made by turning itself into 3 half-size copies at each step:

(iteration 1)

(iteration 2)

(iteration 3)

(iteration 9)

And that definitely doesn't look like the Sierpinski triangle.  Although, it has a similar pattern of holes if you think about it!