Yummmm...

I take back what I said earlier about fractals and food.

First, some fractal pizza (stomach-filling, if not space-filling).

And for dessert, yummy fractal cookies, with instructions here:

Credit:Lenore Edman

The fractal pattern of the cookies would also make a pretty nice quilt pattern!  It's called the Sierpinski carpet, and its Hausdorff dimension is 1.8928.

More Quilts & Sierpinskis!

Thinking about fractals and quilt patterns led me on a google search, which resulted in finding this page - Quilts and Famous Curves - about some real quilts made with fractal patterns.

As far as I can tell, the Sierpinski curve featured doesn't have anything to do with the Sierpinski triangle except that they were both described by the same guy.  Here's a diagram of an alternative method of construction (basically just skipping every other step in the construction given on the quilt page):

Weisstein, Eric W. "Sierpiński Curve." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/SierpinskiCurve.html

You can't directly apply the Moran equation method to find its dimension, because the scaled-down copies that compose the whole overlap with each other a little, and the Moran equation only necessarily holds when they are non-intersecting

According to wikipedia, the curve is space-filling, which means that in the limit as n (the number of iterations of fractalization) goes to infinity, the curve fills up the unit square completely.  This means its Hausdorff dimension is 2, while its topological dimension is 1.  One definition of fractal requires that a fractal have non-integral Hausdorff dimension, so under that definition, the curve isn't really a fractal.  Personally I think Mandelbrot's definition (mentioned in my last post), where a fractal merely has greater Hausdorff than topological dimension, is a lot more useful, because of shapes like this; this shape is certainly not normal, so I think we might as well throw it in with the fractals.  But that's just semantics.

That wikipedia page also says that this curve has been used to make an approximation algorithm for the Travelling Salesman Problem (pretty cool!); it also has some java and logo code for drawing the curve if you're interested.

If you're interested in seeing more mathematical quilts, here is the homepage for one of the authors of the book featured in the first link.  There are lots of neat pictures.

P.S. There is a another fractal curve similar to this one that is directly related to the Sierpinski triangle.  It starts out like this:

 Turn it into a bump made out of bumps:

 And turn each of those bumps into smaller bumps:

Do you see where this is going?

It's the Sierpinski triangle!

(9 iterations)

It's a little bit intuitive, since you are turning the shape into 3 half-size copies of itself at each step, just like in the other construction.  But the shape and placement of the copies does matter; for example, the following fractal is also made by turning itself into 3 half-size copies at each step:

(iteration 1)

(iteration 2)

(iteration 3)

(iteration 9)

And that definitely doesn't look like the Sierpinski triangle.  Although, it has a similar pattern of holes if you think about it!

Self-Similar Fractals: Quilts and the Sierpinski Triangle

This is the first in what I hope will be a sporadic series explaining some of the math behind certain kinds of fractals.  (Well, I hope it will be a series; I don't hope specifically that it will be sporadic, but I'm sure that if it is a series it will be sporadic.)

Self-Similarity
One of the non-technical definitions of "fractal" is "self-similar, and infinitely detailed".  Self-similar means that the parts are similar to the whole; as you zoom in on one part of the fractal, you keep finding properties similar to the properties of the entire fractal.  This can be exhibited in a lot of different ways (there are a lot of different properties with respect to which an object coul be self-similar), and not all fractals have the exact kind of self-similarity I'm writing about in this post.  In this post, I'm writing about fractals that are made up of scaled down, but otherwise exact, copies of the whole thing.

Sierpinski Triangle
Start with a triangle.

In order to be self-similar, it has to be made up of smaller copies of itself.  So turn it into a trangle made out of triangles.

But now those smaller triangles aren't really copies of the whole thing, because the whole thing is made up of smaller triangles, whereas the smaller triangles are just plain triangles!  So, make them into triangles made up of even smaller triangles.

But now the even smaller triangles aren't really copies of the whole thing, because the whole thing is made up of smaller and even smaller triangles, whereas the even smaller triangles are just plain triangles!  So, make them into triangles made up of yet smaller triangles.   But...  won't we end up with the same problem?  Yup.  So what do we do?  Keep going till infinity.

And now in the pursuit of perfect self-similarity, we've also got infinite detail.  And that is the Sierpinski Triangle, a fractal named after Wacław Sierpiński.

Quilts
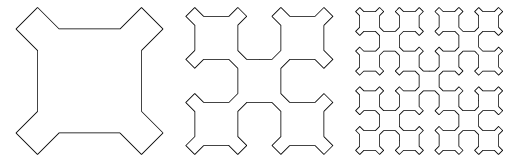
We can do the same kind of process with other shapes to make more cool fractals.  One pattern that I've been playing with recently looks like it would make a neat quilt pattern:

It's made by starting with a square and turning it into smaller squares, and then doing that to each smaller square, like so:

 If I mix things up a bit, and at some steps turn squares into hexagons or circles that have new rules for turning into more circles, hexagons, or squares, I can get things like this:

Some Math
I said before that "self-similar and infinitley detailed" was a non-technical definition of fractal.  There are several technical definitions, and they aren't entirely consistent (a topic for another post?), but the one I'm going to go with is "a set whose Hausdorff dimension is strictly greater than its topological dimension".  (This is the definition Benoit Mandelbrot used (see The Fractal Geometry of Nature).)  If you know about sets and dimensions already, then you have an idea what that means; if you don't, I'll try to explain.

Topological dimension is a usually intuitive notion of dimension that we usually mean when we say "dimension". Look at your hand.  Think about all the points in space that your hand occupies.  That set of points is three-dimensional.  The image represented by the lights of your computer screen, on the other hand, is two-dimensional.  A squiggly (or non-squiggly) line is one-dimensional.  These are topological dimensions.  But, what is the dimension of the Sierpinski Triangle?  Well, it's made up of a bunch of line segments, so its topological dimension is 1.  But we add infinitely many line segments, and it keeps getting denser and denser - might this make the dimension get bigger?  But then, it's never as dense as a filled-in plane... what if we decided to try something wacky and allow dimensions between 1 and 2?  Just to see what would happen?  Hausdorff dimension does just that.  Your hand's Hausdorff dimension is still 2, unless you're an awesome mutant with a fractal hand, in which case I'd love your autograph but I'm not sure you'd be able to write it.  My point is, Hausdorff dimension usually is the same as topological dimension, except in pathological cases (fractals).  The actual definition of Hausdorff dimension is a topic for another time, but I'll write now about how to find the Hausdorff dimension of exactly self-similar fractals (which is a lot easier than in general).

The Hausdorff dimension of an exactly self-similar fractal is found by solving the following equation (called a Moran equation) for $s$:

\[  \sum c_i^s = 1 \]

The $c_i$ terms are the scaling ratios for the self-similarity.  For example, in the Sierpinski Triangle, the whole set of points is made up of three copies of itself, each of which is scaled down to 1/2 the size of the whole, so $c_1 = c_2 = c_3 = $ 1/2.

The Moran equation for the Sierpinski Triangle, then, is
\[ 3\left(\frac{1}{2}\right)^s = 1 \text{, or } \left(\frac{1}{2}\right)^s = \frac{1}{3} \]
We can take the logarithm of both sides and get $ \log(\frac{1}{2})^s = \log\frac{1}{3}$, and then use properties of logs to get $ s = \log\frac{1}{2}/\log\frac{1}{3}$ which is the same as $\frac{\log{3}}{\log{2}}$.  Plug that into wolframalpha, and we find that $ s = $ 1.584962..., and that is the Hausdorff dimension.  Since this is definitely greater than 1, the topological dimension of the Sierpinski Triangle, it is a fractal.

We can do the same thing with my quilt fractal.  It's made up of five copies itself, four of which are scaled down to 1/4 the size, and one (the middle, tilted one) scaled to $(1/\sqrt{2})$ the size.  So the Moran equation is
\[ 4\left(\frac{1}{4}\right)^s + \left(\frac{1}{\sqrt{2}}\right)^s = 1. \]
This is a lot harder to simplify by hand but fortunately wolframalpha can take it from here and give us $s =$ 1.6121...  So that's the Hausdorff dimension of the quilt fractal.  I haven't figured out yet how to apply this to the mixed up hexagon/circle/square fractals.